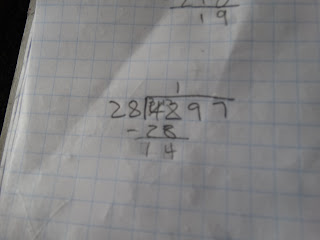Sensorial Exploration of Distributive Law

Nito was presented with an extension of the Distributive Law today.  This brought in the idea of arithmetic exploration.  I apologize in advance for these pictures.  I didn't really how bad the glare was until I put them on the computer.  So, for your reference, the brown cards are 3 and 5 respectively.

The first set of parentheses has the 7 bar and the 2 bar that he will be multiplying by the brown 3 card and the 5 card.  

He first turns over the brown 5 card so that he can multiply both bead bars by the brown 3 card.  He then places his beads below.  

Now, he turns the brown 3 card over and multiplies by the brown 5 card and places the beads below on the right hand side.

He then totals the individual columns and places that below.

He pushes all of the beads together.

Then he simplifies and trades in beads for the final answer.  He ends up with the answer of 72.

CHECK USING COMMUNICATIVE LAW

So the great thing with the Montessori way of learning is that the child always has some way to check his answer.  He doesn't really have to rely on the teacher to know if his answer is correct or not (which is great because I'm not always available!)  For this problem, he can check his work using the communicative law.  

Nito basically just flip flops the beads and the cards.  He now has the 3 and 5 beads on the left with the brown 7 and 2 cards on the right.  The same process is done as before.  The brown 2 card gets turned over and the bead bars get multiplied by the brown 7 card with the answers being placed below.

The brown 7 card is flipped over and now the bead bars will be multiplied by the brown 2 card, placing the beads below.

Sum the columns individually.

Push all of the beads together.

Simplify and trade the beads in for the final answer.  72!  Yay, his answer checks out.

Geometric Multiplication

 

Today I reviewed the concept of geometric multiplication with Bubs.  It is a simple multiplication problem, but the child draws it on graph paper and color codes it.  The problem he started with was 3,748 x 53.  

He first started with drawing the multiplicand of 3,748.  He started in the bottom right hand corner of the paper and made a dot.  Then he counted eight units to the left for the first number of his multiplicand.  He made another dot.  The length of that line represents eight units so he drew a line to connect the dots and wrote an "8" underneath the line.

He continued for the remaining categories of his multiplicand.

Here is the multiplicand graphed on paper.

Next he drew the multiplier.  He started with the same dot as the 8 for the units at the bottom right hand corner of the paper.  However, now he will move upwards counting vertically, instead of across the paper horizontally.  The unit of the multiplier is 3.  He counted up 3 lines and drew a dot.  Connect the lines and write a 3 to the right of the line.  This length represents the three units of the multiplier.  He connected all of the dots to make a rectangle.  He is multiplying so he will multiply the units by the units to get some amount.  How much is 8 x 3?  24.   This equation is written in the rectangle and then colored green for units.

He continues for the remaining categories and colors them according to their category: blue for tens, red for hundreds, and green for thousands.   You should be able to click on the picture to enlarge if the picture is too small.

Now, he moved to the next row vertically to multiply the 50 tens. He multiplied 50 x 8.  That gave him 400 units.  He marked the lines vertically and created another rectangle.  Then he colored it green for the units.  

He continued with the remaining categories in the second row.

The final step is to calculate his answer.  He looked at the products of each area of the diagram and added them together.  He recorded his answer as he added each category.

Stamp Game - Division

Today, I showed Bubs how to do long division using the stamp game.  He practiced writing it down on paper as well.  He tried to jump straight to paper and was struggling a bit, so we brought out the stamp game for reinforcements.  He has pretty much mastered racks and tubes and feels like the stamp game is "baby" work and actually started crying like a "baby" today when I told him to go get it off of the shelf!

Once we moved past all of the tears, he set up his problem.  He divided 4,297 by 28.  The white strip is his division bar.  He lays out all of the tiles for the dividend and writes the divisor on a piece of paper.  (Sorry, the picture doesn't show the number on the white paper very well.)

He uses his button (the green circle above the division bar) to keep track of which category he is working on.  He then asks himself the question, "How many groups of 28 can I make with 4 thousands?"  His answer is zero.

He moves the button over the hundreds category.  The thousands and hundreds get pushed together.  Then he asks his question again.  "How many groups of 28 can I make with 42 hundreds?"  He now needs to exchange one of his thousand tiles for 10 red hundred tiles.

He exchanges his tile and then makes one group of 28.  His remaining tiles are 1 thousand tile and 4 hundred tiles.  

He records his answer on his paper.  He put a 1 above the 2 in his dividend.  He asks the question of how many did he use.  The answer is 28 of 42.  His remainder is 14.  This should match the amount of tiles he has left over.  Ideally, he writes his number on a blank ticket and places it in the correct category column above the division bar along with recording it on his paper.

The button is now moved over the ten category column.  At this point, thousands, hundreds, and tens need to be pushed together.  Remember, since the divisor has two digits, he can only have two different colors, or categories to work with.  He will need to exchange his green thousand tile for 10 hundred tiles.

"How many groups of 28 can I make with 140 tens?"  He starts sharing the tiles and comes up with 5 groups.  He has 9 tiles left over.  Bubs records his answer on his paper.

Now he brings down his final category of units to meet up with his tens that were remaining.  

He shares all of his tiles and is left with 13.

Records it on paper.

This is what the final problem should look like all laid out.  You can see how the categories end up at the bottom by the time you reach the units so the child can visualize that the number needs to be "brought down".  Oh my...just seeing those random pencils in the picture again.  Bubs!  He was obsessed with getting those in the pics.

Large Bead Frame - Multiplication

Today I presented multiplication on the large bead frame to Nito.  He was so excited to do this and actually said it was fun! Ha.  Go figure, math being fun.  He had the biggest grin on his face when he would check his answer and get it right.  The picture above is the large bead frame.  It has categories up to 1 million, unlike the small bead frame which only goes to 1, 000.

Unfortunately, I didn't have (or honestly can't find) the paper specifically for the large bead frame, so he had to use the small bead frame paper.  I just added the columns for tens and hundreds for him.  Ok, so here is his problem.  4,346 x 4.  He first starts with decomposing the number on the paper.  He starts with the units, which is 6.  Then he moves to the tens and records it as 40.  When he has completed decomposing, he makes brackets around the number and writes down what he is multiplying by, which is 4 for this problem.

Now it's time to move the beads on the frame.  The first number is units times the multiplier, which is 6 x 4, or 24.  He moves 4 unit beads to the right and then 2 ten beads to the right to form 24 on the frame.  

He moves to the tens.  4 x 4 which is 16.  He moves the ten beads until he reaches 10, then moves 1 hundred bead to the right, pushes the tens back to the left and keeps counting until he reaches 16.  

The next category is hundreds.   The same process is done, moving a thousand bead when needed.

He finishes up with the thousands and records his answer on his paper.

Here is his paper when he is finished.  He also did a few other problems since he thought it was so much fun and he got them all right.

Distributive Law for Multiplication

Nito was shown another presentation in the sequence for Distributive Law for Multiplication.  It seems that I have never posted anything for the Commutative Law, which is usually a prerequisite for this presentation.  I'll have to get on that!  However, I do show at the end of this presentation how to check your answer using the Commutative Law.

As I mentioned above, he has done the presentations on the Commutative Law, the exchanging of the multiplier with the multiplicand.  For this presentation, I chose a sum of two numbers for the multiplicand.  In the picture above, I chose 5 and 2. Since I am considering it a sum, he puts parentheses around the two bead bars. He will take this sum 3 times.  He uses a brown 3 card and places it on the outside of the parenthesis.  Ok, now ideally the child uses a gray card, but all I had on hand was brown construction paper when I made these materials.  I mean, who has time to drive 45m-1 hour round trip to Michael's with 6 kids just to get gray paper?!  Honestly, it doesn't matter the color paper, as long as it isn't white.

This is the box of bead bars that he uses.  It is a bit different from the checkerboard bead box because this one includes the ten bars.

What does taking this sum 3 times mean?  It means taking the 5 bar 3 times and the 2 bar 3 times.  The blue beads are the 5 bars and the green are the 2 bars.

Then the value is calculated and placed underneath the respective columns (15 and 6).

Then the beads are pushed together.

Now, the beads are exchanged to make a single number of 21.

Commutative Law Check

Since the child knows the commutative law, he can check his answer.  It says if you exchange the multiplier with the multiplicand, then you should get the same answer.  Nito laid out the problem after exchanging beads for tickets and tickets for beads.  In the picture above, the distributive law is on the left hand side and the commutative law is on the right hand side.  He laid out a 3 bead bar and now has a 5 and 2 brown card inside the parentheses. 

He begins by taking the 3 bead bar 5 times and then takes it 2 times.  He finds the answer and places the single number below.

This picture shows that the commutative law on the right hand side has an answer of 21 which matches his distributive law answer of 21.  His work checked out!

Checkerboard

Ah the checkerboard.......It has to be one of my favorite lower elementary materials.  I'm not quite sure why I haven't posted on this yet.  My mother, Gigi, was very kind to make me this checkerboard which can be rolled up and stored like a work rug for the child.  She saved me some precious moolah and also made a decimal checkerboard while she was at it.  It's great to have a supportive grandmother!

The checkerboard has 4 rows and 9 columns of squares arranged in hierarchical colors: green for units, blue for tens, red for hundreds, and green for thousands.  These are the same colors used in previous math materials so the child will be very familiar with them.  The columns range from unit to millions while the individual squares account for units to one billion.  The individual rows not only represent value, they represent the partial products of multi-digit multiplication!  The child can make some large numbers (which Bubs was always excited to do).

Some people are hesitant to start this work for a child if the child has not learned all of his multiplication facts.  However, because the child uses bead bars, there is no need to have the facts memorized.  The child can multiply large numbers while skip counting with the bead bars.  After much use of this material, the facts are mastered. 

Nito has already worked with the checkerboard before.  Today, I presented the 2 digit multiplicand and 2 digit multiplier.  I will walk you through the steps.

The problem is 79 x 12.  He uses the color coded numbers I made for him which correspond to the square on the checkerboard. (Green for unit, blue for ten, etc.)

First, he turns over the ten card for both the multiplicand and the multiplier.  He is focusing on the units first.  He will multiply 9 x 2 which is 18.  He places a brown 8 bar in the units square and a red 1 bar in the tens square.  This now reads "18".  

Second, he turns over the 9 unit card and turn the 7 tens card face up.  Now he is ready to multiply 7 and 2 which is 14.  Now, for the child who is first learning this material, they will focus on the fact that it is 14.  However, as the child progresses, we point out to them that it is really 7 tens and 2 units which makes it 70 x 2.  Therefore the answer is 140, not 14.  This is why you see the yellow 4 bead bar in the tens square and the red 1 bar in the red hundreds square.  The green unit square still only has the brown 8 bar.  

Now the child has successfully multiplied the multiplicand by the unit of the multiplier.  It is time to move on the ten of the multiplier which is the blue 1 card.  The child starts over with the green 9 unit card being flipped over and will now multiply the 9 by the 1.  A blue 9 bar is placed in the ten square above the green unit square.  Remember, we are really multiplying 9 x 10.  This makes the unit have zero and the ten have a 9 bar.

The steps are repeated as before.  The green unit card is flipped over and the blue ten card is face up to now multiply 7 x 1 or really 70 x 10 giving us 700.  We place a white 7 bar in the red hundred square.

The multiplying is complete and now requires us to push all of our beads together.  We do this in an orderly fashion of pushing each column diagonally to the left staying with the same color squares.  For example, the blue 9 bar from the ten square on the second row gets pushed diagonally to the left to end up in the blue 10 square on the bottom row.  Continue with all squares with beads.

Once all of the beads have been pushed to the bottom row, exchanging must begin.  Starting with the units and working left, start exchanging bead bars to end up with one per square. 

The final answer should look like this.  

79 x 12= 948